離散分布是統(tǒng)計(jì)中具有離散值的數(shù)據(jù)分布�����。離散值是可數(shù)的���、有限的����、非負(fù)整數(shù)���,如 1�����、10�����、15 等�����。那么什么是離散分布?這篇文章為大家?guī)?lái)美國(guó)留學(xué)生離散課程詳解���。
一�、了解離散分布
如前所述��,離散型分布是指數(shù)值為可數(shù)整數(shù)的分布�����。另一方面�����,連續(xù)分布包括小數(shù)點(diǎn)后無(wú)限位的數(shù)值����。"π "就是連續(xù)分布中數(shù)值的一個(gè)例子�����。π是一個(gè)小數(shù)位數(shù)(3.14159......)。
這兩種分布都與概率分布有關(guān)��,而概率分布是統(tǒng)計(jì)分析和概率論的基礎(chǔ)�����。
概率分布是一種統(tǒng)計(jì)函數(shù)�����,用于顯示隨機(jī)變量在特定范圍內(nèi)的所有可能值和可能性���。該范圍由最大值和最小值限定��,但實(shí)際值取決于許多因素���。有一些描述性統(tǒng)計(jì)用于解釋預(yù)期值的最終位置。
離散分布也出現(xiàn)在蒙特卡羅模擬中���。蒙特卡羅模擬是一種統(tǒng)計(jì)建模方法����,它通過(guò)運(yùn)行大量模擬來(lái)確定不同結(jié)果的概率。通過(guò)蒙特卡羅模擬�,具有離散值的結(jié)果將產(chǎn)生離散分布,以供分析�。
二、離散分布示例
舉個(gè)例子�,你要計(jì)算在某一小時(shí)內(nèi)走進(jìn)商店的人數(shù)。數(shù)值必須是可數(shù)的����、有限的、非負(fù)整數(shù)���。不可能有 0.5 的人走進(jìn)商店����,也不可能有負(fù)數(shù)的人走進(jìn)商店����。因此,在分布圖上表示的數(shù)值分布將是離散的�。

觀察上述收集到的數(shù)據(jù)點(diǎn)的離散分布,我們可以發(fā)現(xiàn)有 5 個(gè)小時(shí)有 1 到 5 個(gè)人走進(jìn)店里��。此外�,還有 10 個(gè)小時(shí)有 5 到 9 人走進(jìn)商店���,以此類(lèi)推���。
上面的概率分布直觀地顯示了在任何給定的時(shí)間內(nèi)�����,一定數(shù)量的人走進(jìn)商店的概率�。在不做任何定量分析的情況下���,我們可以觀察到����,在任何給定的小時(shí)內(nèi)���,有 9 到 17 人走進(jìn)商店的可能性很大����。
三�����、連續(xù)分布示例
連續(xù)概率分布的特點(diǎn)是具有無(wú)限且不可計(jì)數(shù)的可能值范圍。連續(xù)隨機(jī)變量的概率由概率密度函數(shù)曲線(xiàn)下方的面積定義����。
概率密度函數(shù) (PDF) 是通過(guò)采樣信息推斷連續(xù)隨機(jī)變量取特定值的可能性,并測(cè)量 PDF 下方的面積����。雖然隨機(jī)變量取特定值的絕對(duì)可能性為 0(因?yàn)榭赡艿闹凳菬o(wú)限的),但兩個(gè)不同樣本的 PDF 可用來(lái)推斷隨機(jī)變量的可能性��。
舉個(gè)例子�����,您想計(jì)算某個(gè)人群的身高分布����。您可以收集樣本并測(cè)量他們的身高。但是���,您無(wú)法得出任何一個(gè)被測(cè)量個(gè)體的確切身高���。
在計(jì)算身高分布時(shí),您可以認(rèn)識(shí)到一個(gè)人身高正好為 180 厘米的概率為零。也就是說(shuō)�����,無(wú)限精確地測(cè)量一個(gè)人的身高為 180 厘米的概率為零�����。但是���,可以測(cè)量出一個(gè)人的身高大于 180 厘米的概率。
此外���,您還可以計(jì)算出一個(gè)人的身高低于 180 厘米的概率�。因此����,您可以使用推斷出的概率計(jì)算出一個(gè)范圍值,例如 179.9 厘米到 180.1 厘米之間���。
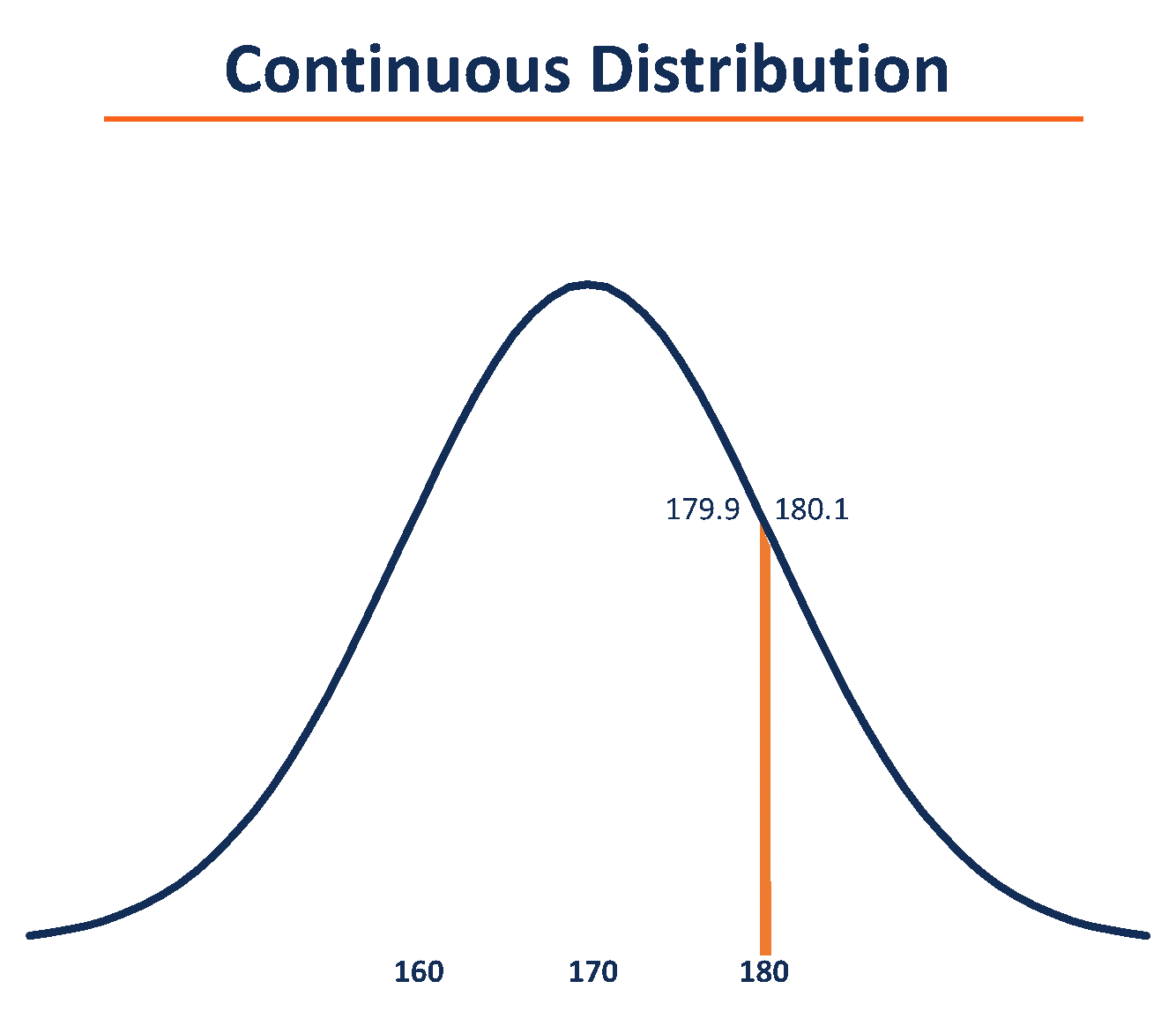
觀察連續(xù)分布����,可以清楚地看到平均值是 170 厘米;但是,可以取值的范圍是無(wú)限的���。因此���,要測(cè)量任何給定隨機(jī)變量的概率,都需要在兩個(gè)范圍之間進(jìn)行推斷����,如上圖所示。
海馬課堂專(zhuān)業(yè)課程輔導(dǎo)���,2100+嚴(yán)選碩博學(xué)霸師資����,針對(duì)學(xué)生的薄弱科目和學(xué)校教學(xué)進(jìn)度����,匹配背景相符的導(dǎo)師,根據(jù)學(xué)生情況進(jìn)行1V1專(zhuān)屬備課�����,上課時(shí)間靈活安排��,中英雙語(yǔ)詳細(xì)講解課程中的考點(diǎn)、 難點(diǎn)問(wèn)題�����,并提供多方位的課后輔導(dǎo)�,輔助學(xué)生掌握全部課程知識(shí),補(bǔ)足短板�����。
相關(guān)熱詞搜索:

![]() 聆聽(tīng)您的聲音:feedback@highmark.com.cn企業(yè)熱線(xiàn):400-778-8318
聆聽(tīng)您的聲音:feedback@highmark.com.cn企業(yè)熱線(xiàn):400-778-8318










 24h在線(xiàn)客服
24h在線(xiàn)客服